Le PPCM
Les tours
Comment trouver le PPCM de deux ou trois nombres en utilisant les blocs.
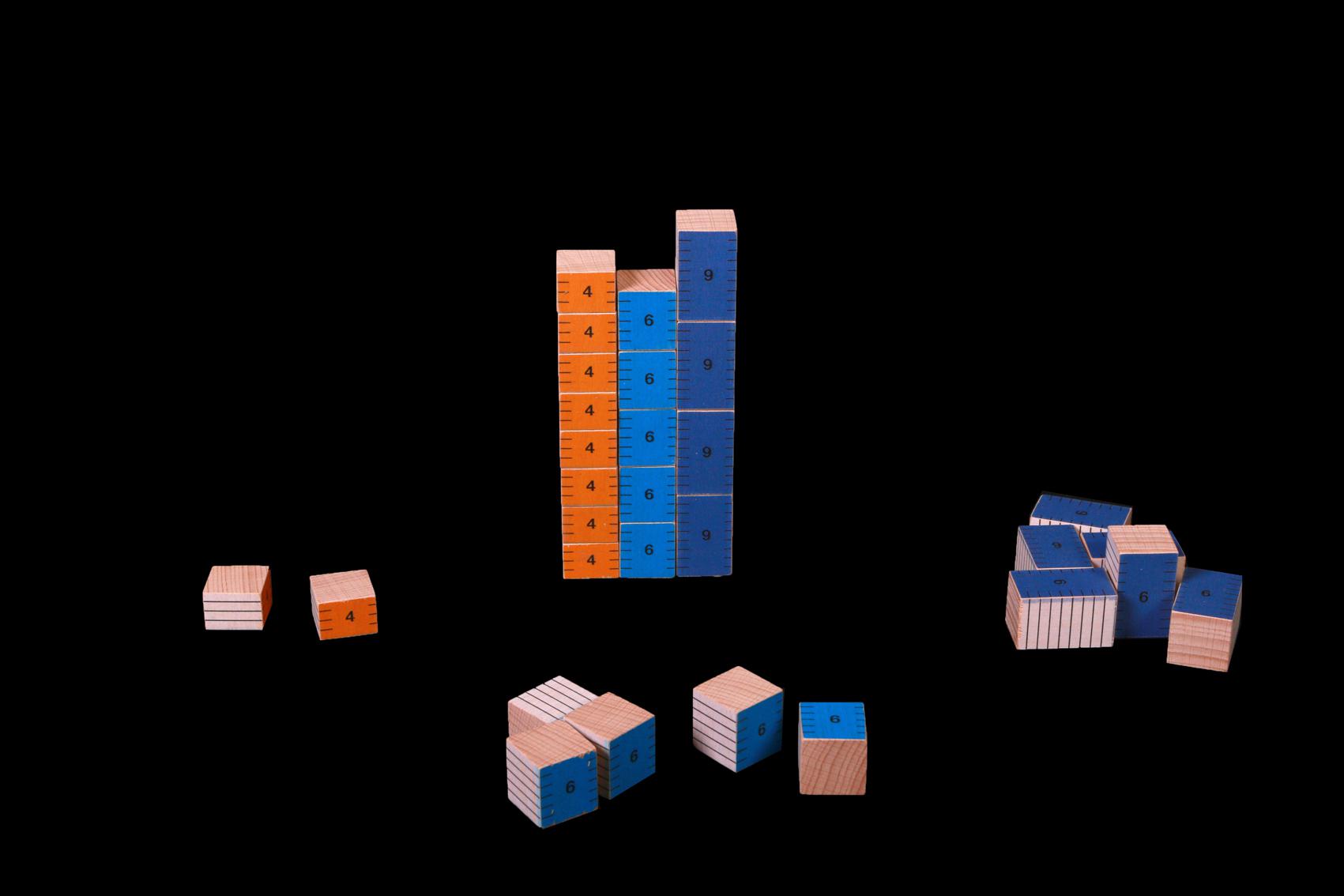
Le PPCM
Les tours
Comment trouver le PPCM de deux ou trois nombres en utilisant les blocs.


Le PPCM
L'arbre
Cette technique permet de trouver sans erreur le Plus Petit Multiple Commun à deux nombres en disposant les multiples des deux nombres de chaque côté de la barre centrale.
Le PPCM
Les escaliers
Comment les escaliers matérialisant les multiples de deux nombres vont-ils se croiser ? Les marches communes sont des multiples communs.
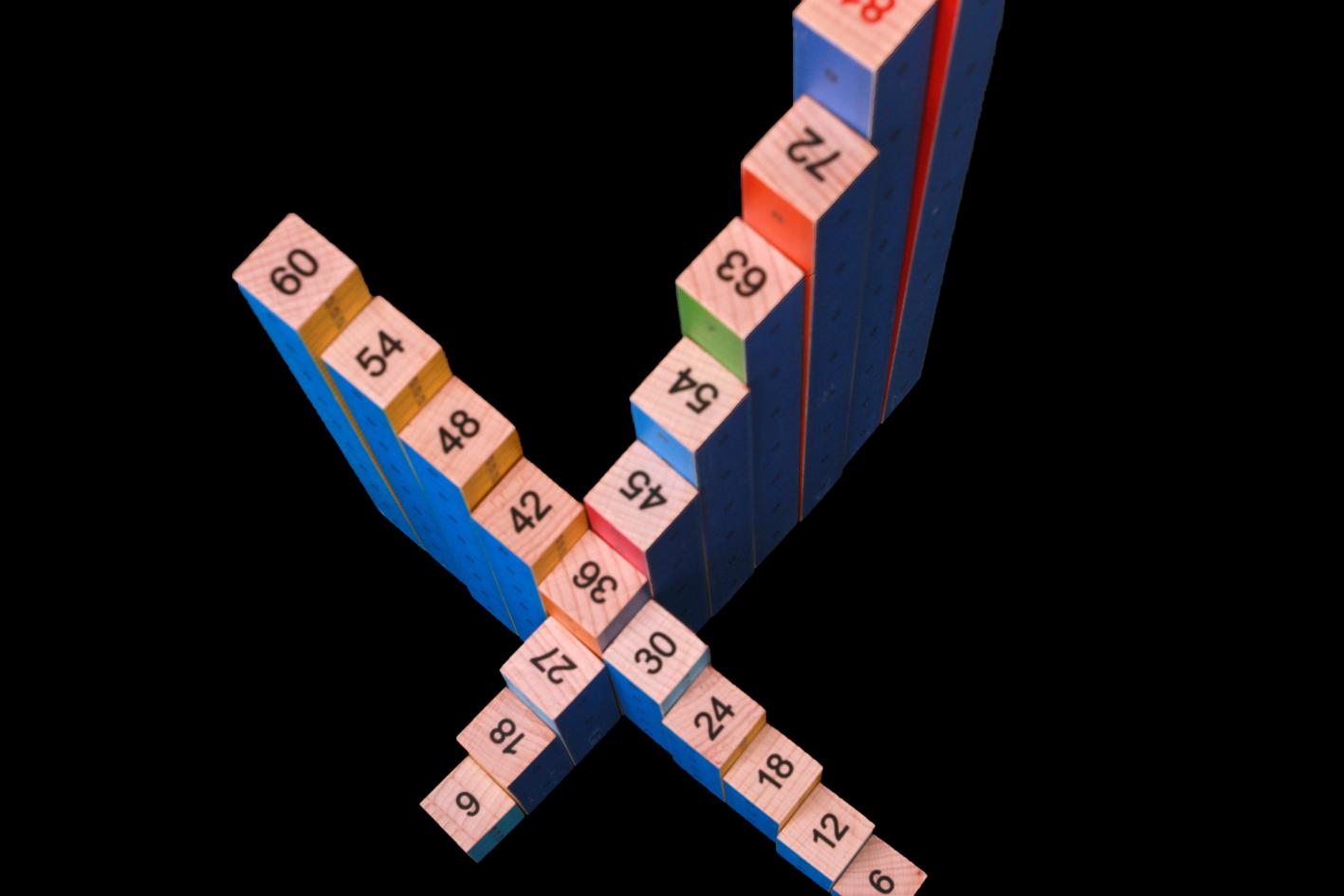

La somme des n premiers nombres
Comment concrétiser la formule qui permet de calculer la somme des n premiers nombres. Voici un exemple pour trouver la somme des nombres jusqu’à 10.
Représentation de fonctions
Des lignes remarquables se dégagent de la table de Pythagore en 3D. Des fonctions du premier et du deuxième degré y sont représentées.
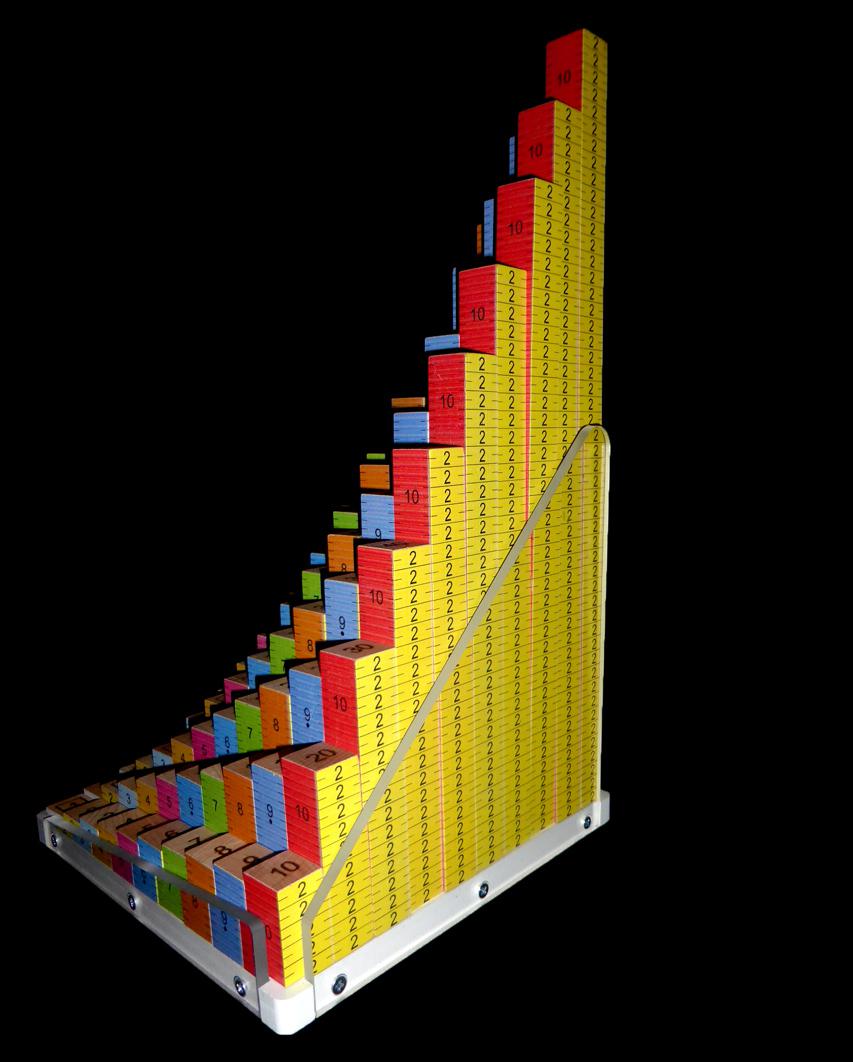

Décomposition de tout entier naturel en une somme de puissances de 2
.jpg?v=1enarbi)
Le théorème de Pythagore
Sans que l’on sache vraiment pourquoi, Pythagore a donné son nom au tableau cartésien rassemblant les résultats des tables de multiplication jusqu’à 10 x 10. Nous allons parler à nouveau du célèbre mathématicien et de son fameux théorème dans cette vidéo.
Nous allons aussi pouvoir toucher du doigt la notion de triangle semblable.


La forme de la pyramide
Des étudiants en maths m’ont indiqué que la table de Pythagore en 3D a une forme bien particulière qui porte un nom : c’est un paraboloïde hyperbolique. J’explique dans la vidéo ce que ce « gros mot » recouvre.
Les nombres premiers
Quand on dispose en ligne le long de la grande barre l’ensemble des 100 résultats de la table de Pythagore, des choses intéressantes apparaissent :
Qu’est-ce qui donne 10 dans la table de Pythagore ?
Comment obtient-on 12 ?
Quelles sont les différentes façons d’obtenir 20 en multipliant deux nombres ?
Et en multipliant trois nombres ?

Ces nombres ne sont divisibles que par 1 et par eux-mêmes. Ce sont des nombres premiers. Ils apparaissent en gris sur une des faces de la règle graduée.
Mais l’observation a ses limites : Tout d’abord 2,3,5,et 7 sont des nombres premiers et ils sont présents en tant que multiplicateurs sur la table, ensuite pour élargir l’observation aux nombres plus grands que 20, il convient de reconstituer les multiples de deux qui sont absents dans la table de Pythagore : il faut ainsi reconstituer le 11x2 =22 et le 13x2=26. On peut alors observer qu’entre 20 et 30, deux nombres entrent dans cette catégorie des nombres premiers, c’est 23 et 29.
La Table de Pythagore - Tous droits réservés - Mentions Légales